Im Nachfeld des Ja zur Masseneinwanderungsinitiative (MEI) wurde vielerorts darüber gerätselt, was die Ursachen der Zustimmung zur Initiative waren. An prominenter Stelle wurden aufgrund bivariater Analysen zwei Gründe gefunden: Im Datenblog des Tages-Anzeigers folgerte Marko Kovic vom IPMZ der Universität Zürich, dass „ein Zusammenhang zwischen dem Ausländeranteil und dem Anteil an Ja-Stimmen [besteht]“ (Beitrag hier), während Peter Moser (stv. Chef des Statistischen Amts des Kantons Zürich, Leiter der Analyseabteilung) in der NZZ die gewachsene Skepsis gegenüber dem bilateralen Weg mit den Raumtypen der Gemeinden erklärte (Beitrag hier). Beide Folgerungen lassen sich in einer multivariaten Analyse der Gemeinden des Kantons Zürich nicht bestätigen.
Doch der Reihe nach. Was ist eine bi- und multivariate Analyse? Eine bivariate Analyse ist letztendlich wenig mehr als das in Verbindung setzen von zwei separaten Variablen. Also: Was für einen Zusammenhang gibt es, wenn ich den Ausländeranteil verschiedener Gemeinden mit der Zustimmung zur MEI derselben Gemeinden vergleiche? Kovic’s Analyse tat genau dies und fand eine negative Korrelation. Je mehr Ausländer, desto weniger Zustimmung. Das Problem dabei (worauf er in seinem Eintrag auch hinweist): Korrelation ist nicht gleich Kausalität. Es kann gut sein, dass wir eine Korrelation finden. Das muss aber nicht heissen, dass sich die Zustimmung wegen dem Ausländeranteil änderte.
Ein Beispiel: Würden wir die Verkaufszahlen von Kleidern in XXL-Grössen in Städten mit der Anzahl Herzinfarkte in diesen Städten vergleichen, würden wir wohl einen positiven Zusammenhang finden. Und zugleich ist klar, dass die Herzinfarkte nicht wegen dem Kleiderverkauf zunehmen, sondern weil die Käufer der Kleider oft übergewichtig sind. Wenn wir aus unserer bi- eine multivariate Analyse machen würden und die Anzahl übergewichtiger Personen konstant halten würden, dann würde der Effekt der T-Shirts auf die Herzinfarkte wohl verschwinden.
Um zu überprüfen, ob die Zustimmung zur MEI tatsächlich mit dem Ausländeranteil und der Zustimmungsschwund zur Bilateralen mit dem Raumtyp der Gemeinde zu tun hat, kann man ähnlich wie im obigen Beispiel vorgehen. Man sucht nach alternativen Faktoren, die einen Einfluss auf die abhängigen Variablen (Zustimmung MEI und Zustimmungsschwund Bilateral) haben könnten, und kontrolliert dafür in einem statistischen Modell. Um das vorherige Beispiel wieder aufzunehmen: Wenn der Effekt des Kleiderverkaufs auf die Herzinfarkte immer noch besteht, wenn man für die Anzahl Übergewichtige kontrolliert, dann ist das ein stärkeres Indiz für einen Zusammenhang, als ohne diese Kontrolle.
Mittels Daten für die Gemeinden des Kantons Zürich wurde der Schritt von einer bi- zu einer multivariaten Analyse der MEI-Zustimmung und dem Bilateralen-Zustimmungsschwund getan. Davon ausgehend, dass dieselben Faktoren auf die Zustimmung zur MEI wie auf den Zustimmungsschwund wirken, wurde das selbe Modell für beide abhängigen Faktoren gewählt.
Verschiedene Faktoren, die im Vorfeld der MEI-Abstimmung als Gründe zum Ja stimmen genannt wurden, sind im Modell enthalten. Diese sind der Ausländeranteil der Gemeinde (Überfremdung wegen Masseneinwanderung), der Pendleranteil (überfüllter ÖV wegen Masseneinwanderung), die Arbeitslosen- und Sozialhilfequote (überlastete Sozialwerke wegen Masseneinwanderung) und die Wanderungsbilanz von Ausländern, Schweizern und aus dem Ausland (sowohl Schweizer wie Ausländer). Ein politischer Faktor, der auf die abhängigen Variablen wirken dürfte, ist die Zustimmung gegenüber der SVP in der Gemeinde. Schliesslich wurden sozioökonomische Faktoren der Gemeinde (Einkommen und Bildung) sowie räumlich-demographische Faktoren (Raumtypen – Stadt, Agglomeration, Land – und Anzahl Einwohner) berücksichtigt.
Der Zusammenhang wird in einem linearen Modell berechnet. D.h. es wird davon ausgegangen, dass der Effekt eines Faktors auf die abhängige Variable konstant bleibt. Da angenommen wird, dass der Einfluss des Einkommens und des Ausländeranteils sich ab einem gewissen Mass abschwächt, wurde für diese Variablen zusätzlich ein quadratischer Term eingefügt. Weiter wird im Modell angenommen, dass der Effekt des Ausländeranteils davon abhängt, ob die Gemeinde eine Stadt, Agglomeration oder auf dem Land ist. Kulturelle Faktoren, die schwer in einem statistischen Modell zu fassen sind, könnten dafür sorgen, dass eine Zunahme des Ausländeranteil in der Stadt einen ganz anderen Einfluss auf die Zustimmung zur MEI hat als auf dem Land.
Wie bewährt sich das Modell hinsichtlich der MEI? Bestätigt sich Kovic’s These auch nach Kontrolle für verschiedene Faktoren? In tabellarischer Form sind die Resultate der Regression hier dargestellt, während unten der Einfluss der Faktoren auf den Ja-Anteil graphisch dargestellt wird. Signifikant (d.h. wir können davon ausgehen, dass der wahre Wert des Zusammenhangs mit einer hohen Wahrscheinlichkeit nicht null ist) wirken der Anteil SVP-Stimmen (Lesebeispiel: Pro 1% mehr Wähleranteile der SVP in den NR-Wahlen 2011 steigt der Anteil der Zustimmung 2014 um 0.71%), die sozioökonomischen Faktoren und die Wanderungsbilanz der Schweizer. Nur auf den ersten Blick signifikant ist der Ausländeranteil: In den Städten ist der Effekt negativ, in der Agglomeration und auf dem Land verschwindet dieser Effekt. Das zeigt sich in den Faktoren „Agglomeration * Ausländeranteil“ und „Land * Ausländeranteil“ in der Regression mit allen Raumtypen (diese Effekte sind positiv, während der Ausländeranteil in der Stadt negativ wirkt) oder aber, wenn wir die Regression nach Raumtyp unterschieden durchführen (Grafiken „Agglomeration“ und „Land“). Hierbei ist der Ausländeranteil jeweils nicht signifikant. Kurz: Kontrollieren wir mit den genannten Faktoren für die Gemeinden des Kantons Zürich, dann hat der Ausländeranteil in der Agglomeration und auf dem Land keinen Einfluss auf die Zustimmung zur MEI in diesem Modell.
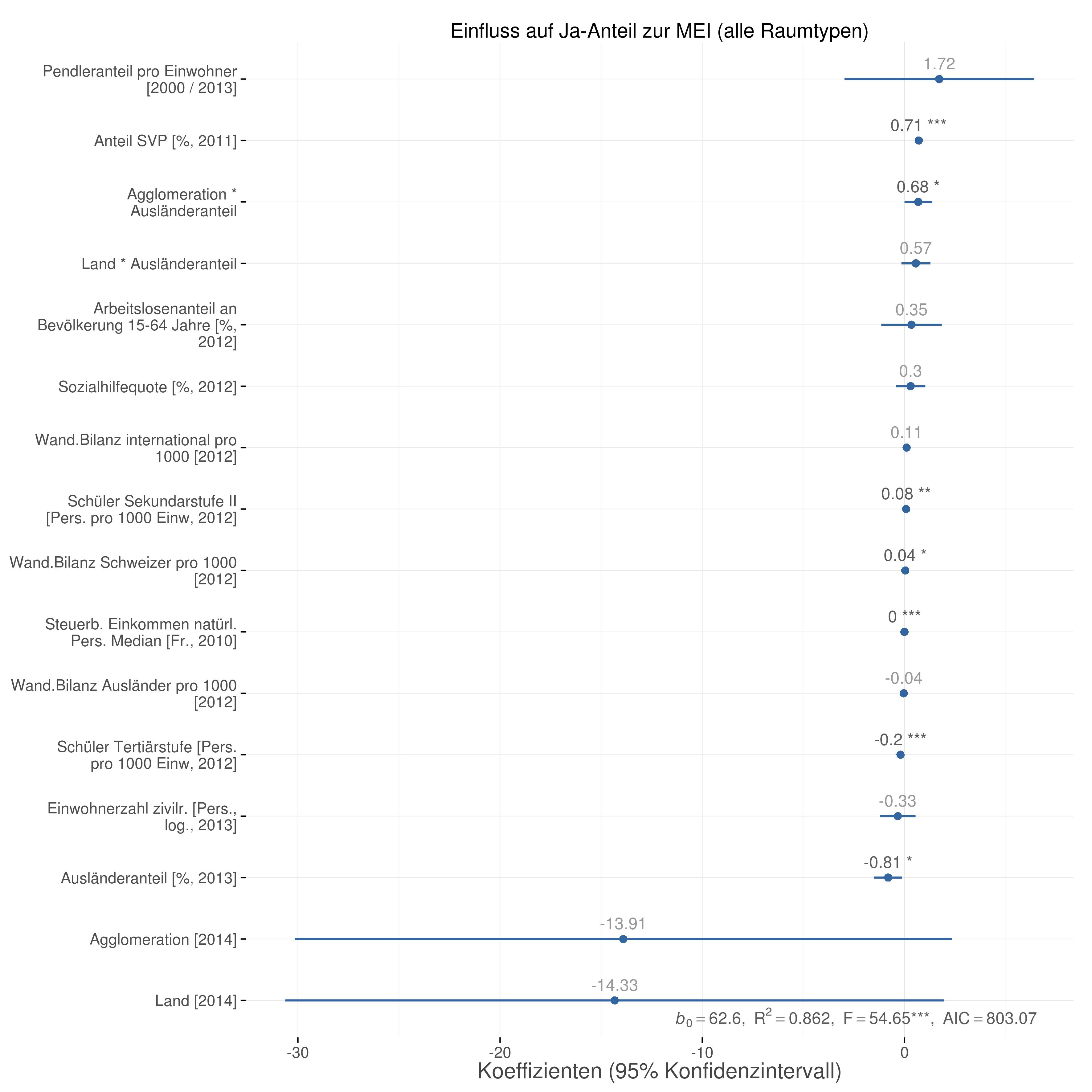
Was ist von Moser’s These zu halten? Für die Zustimmung zur MEI macht der Raumtyp der Gemeinde nichts aus. Was aber, wenn wir den Zustimmungsschwund als abhängige Variable wählen? Der Zustimmungsschwund wird bei Moser als Differenz zwischen der Ablehnung der Abstimmung über die Bilateralen 2000 und der Zustimmung zur MEI 2014 berechnet.
Auch hier lässt sich die aufgestellte These nicht bestätigen (Resultate in tabellarischer Form hier). Das Modell zeigt keinen signifikanten Effekt für den Raumtyp der Gemeinde. Auch wenn wir nur die Gemeinden der Agglomeration bzw. des Landes gegen diejenigen der Stadt vergleichen (Grafiken „Stadt vs. Agglomeration“ und „Stadt vs. Land“), lässt sich kein Effekt beobachten.
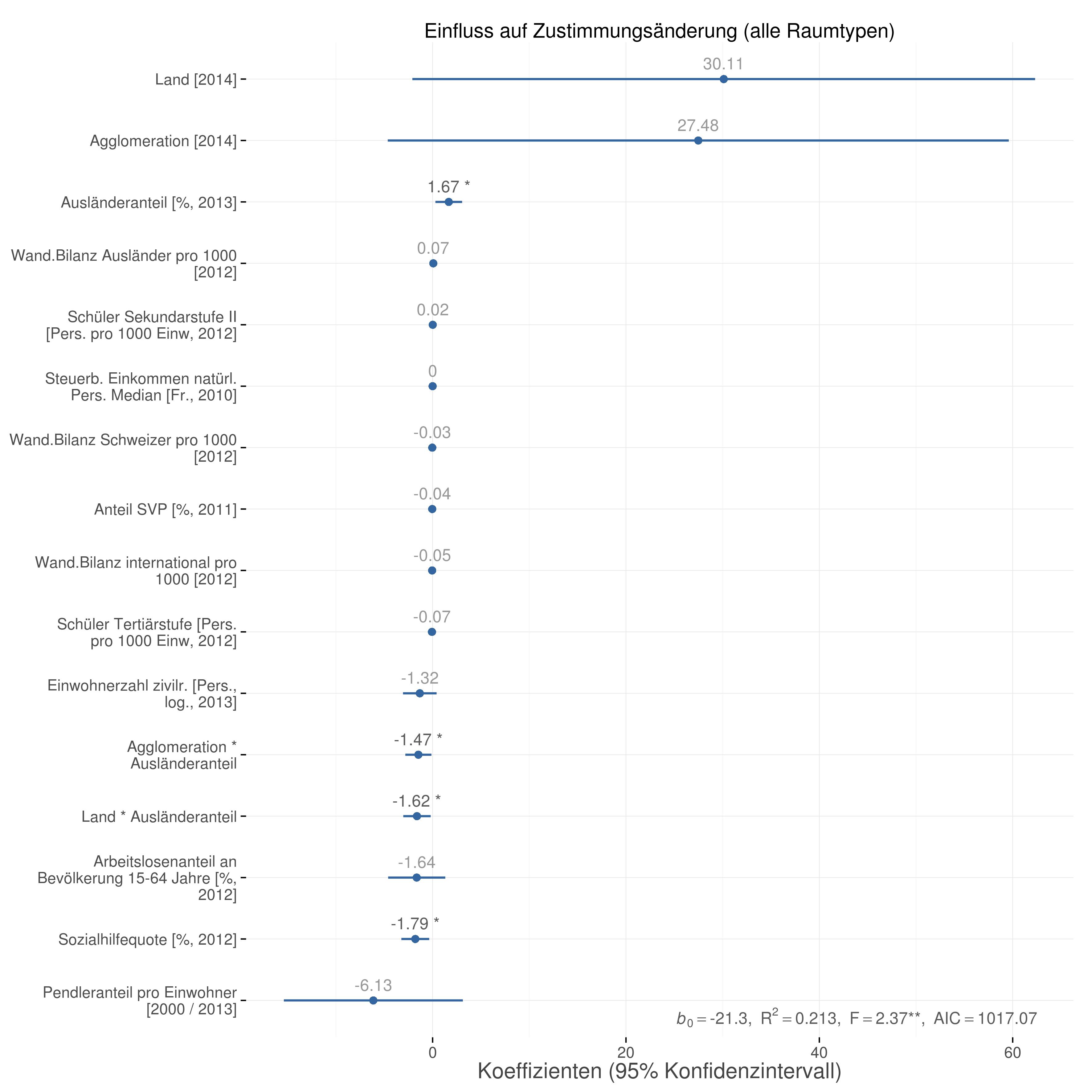
Aber: Das Modell eignet sich grundsätzlich nicht sonderlich gut, um den Zustimmungsschwund zu ergründen. Ersichtlich wird dies über die Werte des R² bzw. des adjusted R². Diese Werte zeigen auf, wie viel der Varianz der abhängigen Variable sich mit dem Modell insgesamt erklären lässt. Die Werte liegen immer zwischen 0 und 1, je näher bei 1, desto besser die Erklärungskraft. Das adjusted R² korrigiert dabei zudem für die Fallzahl in der Berechnung. Liegt es bei der MEI-Zustimmung bei zwischen 0.74 und 0.85, so ist der Wert beim Zustimmungsschwund nur zwischen 0.01 und 0.12. Das liegt wohl an der von Moser genannten subjektiven Wahrnehmung von vermeintlichen Folgen der Einwanderung. Die tatsächlichen Zahlen der Faktoren, die als Argumente pro MEI genannt wurden, haben wenig mit ihrer Annahme zu tun. Der weitaus stärkste signifikante Effekt ist derjenige des SVP-Anteils in der Gemeinde. Erklärungen des Zustimmungsschwunds, die lediglich auf wirtschaftlichen Zahlen beruhen, haben einen entsprechend schweren Stand. Es muss auf subjektiver, d.h. auch politischer, sozialer und kultureller Ebene verstanden werden, warum welche Faktoren heute als Probleme wahrgenommen werden, die früher keine waren. Alles andere greift zu kurz.